Run For Your Life!
It’s time to answer the age-old question of who would win between an Olympic sprinter, tortoise, car, you, and a volcano.

Let’s face it, humans more often than not are fairly confident in their own abilities. With well known volcanic eruptions happening in both Hawaii and Guatemala in 2018, many people most likely feel like they know how to keep themselves safe. But do they really? Hawaii’s Kīlauea and Guatemala’s Fuego were two volcanoes that had very different impacts on the infrastructure and lives in the surrounding areas. If you were around both of these volcanoes when they erupted, survival may not be guaranteed. Many residents in these areas escaped, but is simply putting on your shoes and running away a realistic option in either of these scenarios?
Types Of Volcanoes
The world contains a variety of different types and they vary in a variety of ways including shape and explosiveness in terms of eruptions. Kīlauea is a shield volcano. Shield volcanoes have a shorter profile, cover a greater area, and aren’t known for violent eruptions. This may not seem like a big difference, but their shape is a great indicator of the type of eruptions they have.
Stratovolcano vs. Shield Volcano
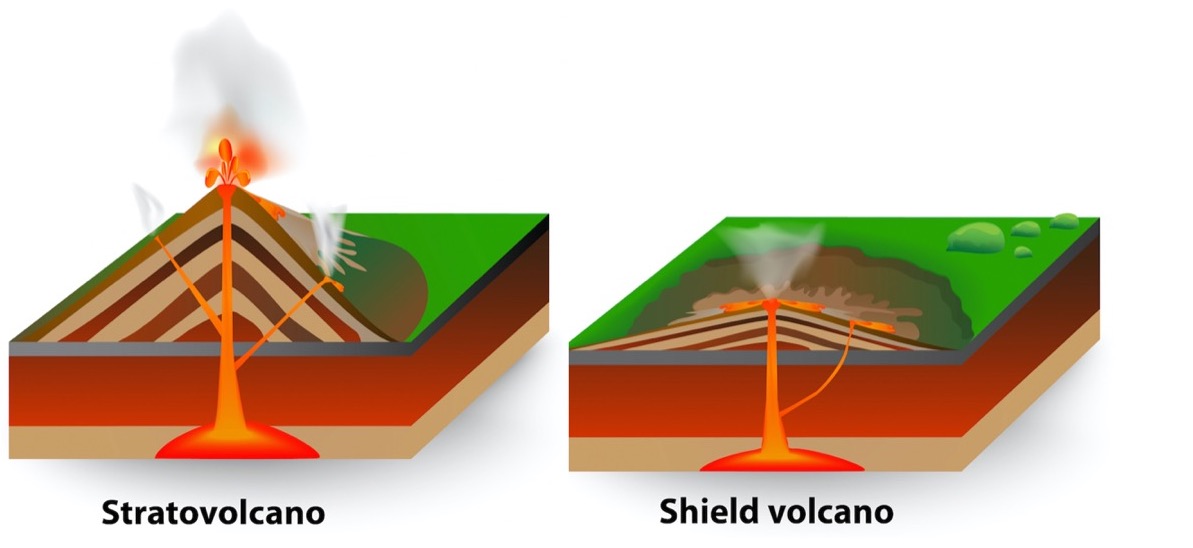
Shield volcanoes are short and round because when they erupt, lava typically flows out from the summit crater due to the fluid-like consistency of the lava. This allows the lava to flow outward like a superheated river for long distances rather than stacking up on top of itself. This ultimately creates a vast volcanic mound, or “shield” instead of the stereotypical tall and triangular mountain shape that may come to mind when thinking of a volcano.
Types Of “Flows”
How quick you need to be when it comes to lacing up your kicks also comes down to what type of lava flow is coming your way. As mentioned earlier, shield volcanoes don’t have that same cone shape due to a lava that is more fluid-like. The more fluidic lava leads to eruptions that are characterized by a steady flow from the volcano’s crater. These flows can drastically reshape a landscape and often travel similar to like a river of molten rock.


Stratovolcanoes don’t have lava with the same composition as shield volcanoes, so their eruptions don’t act the same way as those of shield volcanoes. When a stratovolcano erupts materials that compose the volcano itself, ash ejected in the eruption, and the thicker lava comes together to form a pyroclastic flow. Pyroclastic flows can form a variety of ways and often travel at high rates of speed down a mountainside. These flows are not composed of just lava as many people may think, but instead are flows of superheated debris that travel at incredible speeds. There are a few famous examples of the destructive power in human communities and loss of life from these types of flows, such as the famous Mount Vesuvius and the victims in the nearby city of Pompeii.
The U.S. Geological Survey is the federal organization that, in addition to a multitude of others things, monitors, studies, and informs the public of these type of major geologic events. U.S. Geological Survey geologist Elizabeth Westby has studied many geologic formations and events. The numerous differences in the composition of the lava can have a drastic impact on the violence and speed of eruptions.

Can You Make It?
Let’s imagine that you, a self-driving car, Bertie the World’s Fastest Tortoise, and Usain Bolt are all hanging out in the same town listening to Science Friday when a volcano erupts. If you all are 1 km from the volcanic flow, can any of you escape the resulting lava flows from a volcano like Fuego or Kīlauea? Assume when thinking of this scenario that anyone who is in it can maintain their speed, and their escape route is a flat unobstructed route along the way. Could they make it to safely to the evacuation transport waiting for them in the next town 5 km away from Kīlauea’s lava flow? How much of a head start would they need in order to make it to that safe distance from that much faster pyroclastic flow of Fuego in Guatemala?

To find out, you’ll need to compare the rates that each of these flows is moving by creating and graphing a slope-intercept form equation. We’ll use several benchmarks of some of the fastest things or creatures in the world, including you, as well as one of the slowest. We can then use some information, videos from the internet, and our own data to find out how quickly the different things and creatures move and create a set of equations to model their speed. Finally, we can graph the speed of our characters to the flows of each volcano to determine who will make it and who will not to the safe distance 5 km away.
Materials
Materials required (per student/group of students):
- Copies of student handouts (electronic or printed)
- Copies of the graph paper
- Ruler or another type of straight edge
- A computer or project for the classroom so students can watch the video of Bertie the tortoise and Usain Bolt to gather the information needed to determine their speed. If technology isn’t available to do so, students can also be given the speed of each character before starting.
- Stopwatch (a hand-held stopwatch, timer on a wristwatch, or an app on a smartphone all work great)
- Meter stick
- Optional: Computer/Chromebook/iPads for each student or group of students to be able to access the electronic version of the document and watch the videos linked below to gather information for the student handout.
- Optional: Simple scientific calculators such as TI-36 or graphing TI-83 depending on resources
- Optional: DESMOS may also be helpful in lieu of calculators to graph slope intercept equations. (Click here for a DESMOS tutorial if you’re unfamiliar with it)
Let’s Meet Our Speed Demons!
We’ll be calculating the speed of each of these characters to create a comparison relative to how fast the lava and pyroclastic flows are moving. You can use the guide here to fill out as you go.
| Determine the speed of the world’s fastest tortoise in meters per minute from the following video.
|
Determine Usain Bolt’s speed in meters per minute from the following video.
|
| Convert the average US Interstate speed limit of 65 mph to meters per minute.
|
Calculate your own speed by measuring out a 10 meter distance and having a friend or classmate time you. Calculate your own speed in meters per minute by measuring out a 10 meter distance and having a friend or classmate time how long it takes you to run 10 meters, and then calculate your speed.
|
Image Credits: Giphy
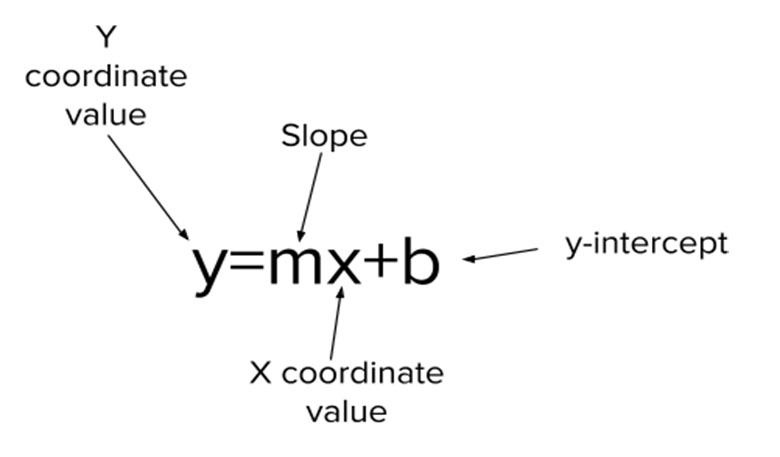
Slope-Intercept Form
Slope-intercept form is a form of linear equation that describes the starting point of a graph based on its placement on the y-axis and the rate of change of its equation. It’s widely used and appreciated because it makes it fairly easy to graph linear functions by easily identifying the y-intercept as a point to start your graph and then using the slope to determine the next points. Each variable in the equations represents a different component of your graph the following way.
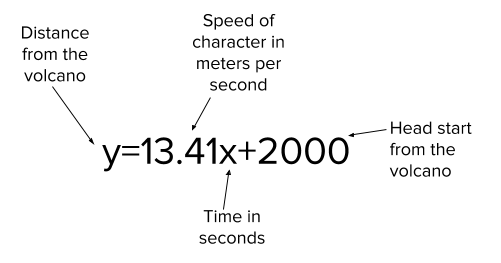
Example: A deer running from the volcanic eruption 2,000m from the volcano at 13.41 meters a second would have a slope-intercept form equation of y=13.41x+2000
Slope-intercept example Credit: Brian Soash
| Kīlauea | Fuego |
|---|---|
| Slope Intercept Form Equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano |
Slope Intercept Form Equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano |
| ______=______x+______ | ______=______x+______ |
| Tortoise Equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano ______=______x+______ |
100m world record holder equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano ______=______x+______ |
| Average Vehicle Equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano ______=______x+______ |
YOUR Equation y=mx+b y=the distance from the volcano m=the speed in meters per second x=time, in seconds b=starting distance from the volcano ______=______x+______ |
Compare The Flows
Lava flows and pyroclastic flows differ from one another in both their speed and composition. The student handout will help you set up and find your calculations of the speed of the lava flow and pyroclastic flow as well as each of the four characters listed above. Next, use the velocity you found for the two volcanoes from the first page of your student handout to create a slope-intercept equation for each volcano and then graph both volcano equations on your graph paper to compare both speeds visually.
Try this: Be sure to start from your y-intercept, or starting distance from the volcano, and then plug in the safe distance of 5,000m into your y-value in the slope-intercept equation to calculate how long it will take each flow (x) to reach the safe distance.
- Observation: If you were only given the graph of the two equations representing the speed of Kīlauea lava flow and Fuego’s pyroclastic flow, how would you know which volcanic flow was moving fastest?
- Analyze: If you expanded the graph of your equations to a four-quadrant graph ,the only place they would intersect would be at your point (0,0) as they do on your graph now. What does the origin on your graph in this situation represent?
- Analyze: Why is the origin the only place that the two graphs of flow speed will ever intersect?
Kīlauea
Using a sheet of graph paper let’s determine whether or not the tortoise, Usain Bolt, a car on a U.S. Highway, or YOU could outrun Kīlauea’s lava flow with a 1,000m head start to a safe distance 5,000m away. Graph Kīlauea’s lava flow and each of the four other equations (tortoise, Bolt, car, yourself) on the graph paper. Be sure to use a different color or type of line for each of your equations, then label them in the key provided.
REMEMBER: Assume that both you and the lava flow travel at your respective speeds in the same direction for the entire time. You can also assume that from your 1000m head start from the lava flow behind you, that you can travel in an even, straight, and uninterrupted line to the safe location 5,000m away.
- Observe: Based on the four equations you graphed, which of our characters, if any, were able to make it to safety 5,000m away before Kilauea’s lava flow arrived there?
- Observe: Were there any characters that made it to the 5,000m mark on your graph paper? If so, what would it mean for that character? Why do you think that was the case? Use evidence from your graph or equation to justify your claim.
- Analyze: How were you able to interpret from your graph if some of our characters did indeed make it to the safety distance of 5,000m away before the lava flow did? Use specific observations you made about the equations from the graph to support your reasoning.
Fuego
Using your same graph paper page and some calculations let’s determine if you could make it to your safe point 5,000m away with your previous 1,000m head start. If not, we’ll find out how much of a head start you would need to reach the safe distance of 5,000m away from the volcano before Fuego’s pyroclastic flow could make it there.
- Observe: Out of the four character’s equations graphed, which one(s), if any, were able to make it to the safety distance of 5,000m away before the pyroclastic flow?
- Analyze: How were you able to interpret which runner was able to escape from the graph?
As mentioned earlier, volcanic eruptions, especially pyroclastic flows, are incredibly destructive. In this scenario it was unlikely that any of our characters were going to survive the fast-moving pyroclastic flow. What type of head start would it take for our 4 characters to survive and make it to the safe distance 5,000m away? Use this example calculation and the data you’ve already collected from the previous section to help you find out the minimum head start the four brave characters in this scenario would need to at least make it to the safe location 5,000m away before the time the pyroclastic flow did.

Reflection
A) Quite a few people live in communities that are very close to one or more volcanoes. Based on what you’ve seen from these two different, but very real situations, would you recommend that people develop communities near or at the base of a volcano? Create a claim and justify your decision using the evidence from the graphs and calculations you created above.
Complete this sentence: “I think that people SHOULD/SHOULDN’T be allowed to develop communities near the based of the volcano because…”
Now list at least three pieces of evidence from the resource, graph, or your calculations from the activity above. Explain how each piece of evidence supports your claim.
B) You’re the governor of a state that wants to build a new housing development on land at the base of an active volcano that hasn’t been previously developed. The law in your state says that currently, it’s illegal to build within 10 miles of a volcano. The developers think you should repeal the law and allow them to build due to a new “Volcano Siren” that’s been developed that will warn the community 15 minutes before an eruption. As governor, what is your decision?
Extension Project Based Learning Opportunity:
Modify the “virtual notebook template” provided to allow students to take what they’ve learned and expand it into a project where students generate potential solutions to one of the needs below.
A) Design an early warning system for communities that live around the base of either of the volcanoes to warn residents quickly in the event of an eruption.
B) Determine zones around each volcano that could be evaluated on safety from an eruption and whether or not communities should be allowed to be built there.
C) Come up with evacuation plans for these or other areas with active volcanoes. Remember, in our experiment we assumed we had a straight and unobstructed path to escape when in truth, real-life situations are very different.
Standards
CCSS.MATH.CONTENT.8.EE.C.8
Analyze and solve pairs of simultaneous linear equations.
CCSS.MATH.CONTENT.8.EE.C.8.A
Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.
CCSS.MATH.CONTENT.8.EE.C.8.C
Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.
NGSS MS ESS2:
Construct an explanation based on evidence for how geoscience processes have changed Earth’s surface at varying time and spatial scales. [Clarification Statement: Emphasis is on how processes change Earth’s surface at time and spatial scales that can be large (such as slow plate motions or the uplift of large mountain ranges) or small (such as rapid landslides or microscopic geochemical reactions), and how many geoscience processes (such as earthquakes, volcanoes, and meteor impacts) usually behave gradually but are punctuated by catastrophic events. Examples of geoscience processes include surface weathering and deposition by the movements of water, ice, and wind. Emphasis is on geoscience processes that shape local geographic features, where appropriate.]
Educator's Toolbox
Meet the Writer
About Brian Soash
@BSoashBrian Soash was Science Friday’s educator community leader. He worked to connect educators, schools, and districts with the outstanding educational content being developed by Science Friday.




